 |
 |
« geri |
| Ədəd (yuxarı) – İrrasional ədədlər |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| İzahı | İrrasional ədədlərin sadələşdirilməsi | Kəsrin məxrəcinin irrasionallıqdan azad edilməsi | Məsələlər | Məxrəcin irrasionallıqdan azad edilməsi | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| İzahı Sonsuz dövrü onluq kəsr şəklində göstərilə bilməyən ədədlərə irrasional ədədlər deyilir. Beləliklə, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| İrrasional ədədlərin sadələşdirilməsi a. Toplama və çıxma Qayda: Yalnız eyni ədədlərin kvadrat köklərini toplaya və ya çıxa bilərik.
b. Vurma və Bölmə Qayda: İrrasional ədədləri vura və bölə bilərik.
İrrasional ədədləri tam ədədlərə vurduqda və ya böldükdə bu qaydadan istifadə edə bilərik. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vürüğun kök altından çıxarılması
Kvadrat kök daxilindəki ədədin vuruqlarından biri kvadrat ədəddirsə, onda kvadrata vurula və kənara çıxardıla bilər. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| İrrasional ədədlər üzrə məsələlər Misal 1: Düzbucaqlının uzunluğu (2 + 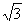 )sm, eni isə (3 – )sm, eni isə (3 – 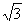 )sm-dır. Düzbucaqlının sahəsini tapın. )sm-dır. Düzbucaqlının sahəsini tapın.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Məxrəcin irasionallıqdan azad edilməsi. Bu məxrəcin irrasionallıqdan azad edilməsi üsuludur.
Qayda: Məxrəci rasional etmək üçün surət və məxrəci - məxrəcin qoşmasına vuraq lazımdır. Misal 2: Məxrəc ifadə olduqda.
Qayda: Kəsrin məxrəcini irrasionallıqdan azad etmək üçün kəsrin surət və məxrəcini məxrəcin qoşmasına vurmaq lazımdır. This eliminates the surd from the denominator. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Copyright ©2015 Edumedia LLC | |
| skoool haqqında Tərəfdaşlar haqqında Toxunulmazlıq və Təhlükəsizlik | |
| EDUMEDIA şirkəti tərəfindən adaptasiya olunub. |
 |
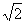 irrasional adlanır.
irrasional adlanır. 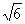 ÷
÷ 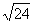 = 2
= 2