skoool™.az

skoool-un dərslərinə tez keçid.

Mikrodalğalar

Fotosintez prosesində yarpağın rolu

Elektromaqnit radiasiyası

« geri

Ədəd (orta) – Ədədlərin praktik istifadəsi

Valyuta kursları

Bu düz mütənasibliyin praktik istifadəsidir.

Misal 1:£1 = €1.5 verilmişdir, €10 avroya çevirin.

£10 = 1.5 x 10 = €15

Misal 2: €28 funta çevirin.

	€ 1 = £1/1.5
	€28 = 1/1.5 x 28 = £18.67 (ən yaxın penniyə qədər)

Qayda: Dəyişdiyiniz pul vahidində bir vahidin nə qədər olduğunu müəyyənləşdirin. Sonra dəyişdiyiniz məbləğə vurun.

Sadə faizlər (I)

Bu faizlərdən praktik istifadədir. Bu investisiya üzrə qazanılmış faizin işlənib hazırlanma üsuludur.

Sadə faiz üçün düstur budur:	I = PTR 100

Burada
P = Əsas (qoyulan pulun miqdarı)
T = Vaxt (il ilə)
R = Faiz norması (%)

Misal 1: 8 ilə müddətinə 15% sadə faizlə £600 kapital qoyulmuşdur. Nə qədər faiz qazanılacaq? 8 ildən sonra məbləğ nə qədər olacaq?

P = 600
T = 8	I =	600 x 8 x 15 100
R = 15
	I =	£720
	Məbləğ =	600 + 720 =	£1320

Qeyd: bu mövzu üzrə suallar I, P, T, və ya R üzrə soruşula bilər.

Sadəcə tələb olunan şərti düsturun predmeti (əsas üzvü) edin və verilmiş qiymətləri yerinə qoyun.

Misal 2: Bir il altı aylıq £6,000 investisiya qoyulmuşdur. Qazanılmış sadə faiz £1,000 olsa, faiz norması nə qədər olar?

P = 6000
T = 1½ il	R =	100 I PT			R-i əsas üzv edin
R = ?
I = 1000
	R =	100 x 1000		= 11	1/9
		6000 x 1½
	R=	11	1/9 %

Mürəkkəb faizlər

Bu halda əldə olunan faiz hər ilin üzərinə əlavə olunur və növbəti ilin faizi tapılır.

Misal 1: 3 il üçün 5%-dən qoyulmuş £900 mürəkkəb faizini tapın.

1ci il 5/100 x 900 = £45

2ci il 5/100 x 945 = £47.25

3cü il 5/100 x 992.25 = £49.61 (ən yaxın penniyə qədər)

Cəmi mürəkkəb faiz = 45 + 47.25 + 49.61 = £141.86

Misal 2: 3 ildən sonrakı məbləği hesablayın.

Məbləğ = 900 + 141.86 = £1,041.86

Daha çox il üçün qısa metoddan istifadə edirik.

Bu misalda rəqəmlərdən istifadə edərək:

Birinci ilin sonunda məbləğ = 105% of 900 = 1.05 x 900

İkinci ilin sonunda məbləğ = birinci ilin 105%-i = 1.05 x 1.05 x 900

Beləliklə, hər ili vururuq 105% = 1.05

Yekun məbləğ = (1.05)³ x 900 = £1,041.86

(Qeyd: bu kalkulyatorda aşağıdakı kimi edilə bilər)

1.05 (qüvvət düyməsi) 3 x 900
^

15 il üçün biz sadəcə qüvvəti 15-ə dəyişirik.

(1.05)¹⁵ x 900 = £1,871.04 (ən yaxın penni)

Sürət

Sürət vahid zamanda gedilən məsafəyə deyilir.

Misal 1: Maşın iki saatda 150 km gedir. Onun orta sürəti nə qədərdir.

	1 saatda maşın 150 ÷ 2 = 75 km
	Sürət = 75 km/saat

Sürətin ölçü vahidləri km/saat və ya m/saniyə ola bilər.

Note: always use the units asked for in a question.

Misal 2: Hissəcik 0.5 dəqiqədə 30000 sm gedir. m/san ilə sürət nə qədər olar?

30000 sm =

0.5 dəq =

Sürət =

300 m

30 san.

300/30 = 10 m/san

Orta sürətin (V) düsturu

S = D
T

burada S = Sürət
D = Məsafə
T = Zaman

Bu düsturdan istifadə etmək üçün iki qiymət verilir. Düsturda sürəti dəyişməklə üçüncünü hesablaya bilərik.

Misal 3: Maşın 2 saat 80 km/saat sürətlə gedir. O nə qədər məsafə qət edir?

S = 80
T = 2
D = S x T (D-ni əsas üzv edirik)
D = 80 x 2 = 160 km

Misal 4: Maşın 60 km-saat sürətlə 300 km gedir. Onun getdiyi məsafə nə qədər olar?


S =	60
D =	300
T =	D
	S (D-ni əsas üzv edirik)
T =	300 = 5 saat
	60

Sıxlıq

Sıxlıq hər həcm vahidinə düşən kütlədir.

Sıxlığın (D) düsturu
D = M
V
burada M = kütlə (g) V = həcm (sm³)

Misal 1: Bərk maddənin kütləsi 500 q, həcmi isə 1000 sm³-dir. Sıxlığı hesablayın.

M = 500
V = 1000
D = 500 = 0.5 q/sm³ 1000

Misal 2: V = 3000 sm³, D = 0.2 q/sm³, so M = ?

M = D x V (M əsas element kimi)
M = 0.2 x 3000 = 600 q

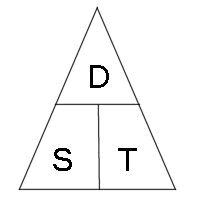
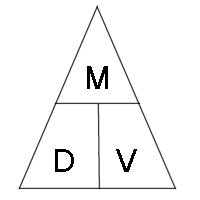
Üçbucaq metodu

Sürət və sıxlığa aid məsələlərin hər iki növü üçbucaqdan istifadə olunaraq həll oluna bilər. Bu Sürət və Sıxlıq üçün Üçbucaq Metodu kimi məlumdur.

Sürət

Üçbucaqdakı şaquli xətt vurmanı, üfüqi xətt isə bölməni göstərir.

Beləliklə, S, t və ya v-in qiymətlərindən ikisi məlumdursa, onda aşağıdakılardan istifadə edərək digərini tapa bilərsiniz.

S/T = V

S/V = T

V x T = S

Sıxlıq

Sıxlıq üçün üçbucaq eyni üsulla istifadə olunur.

M/D = V

M/V = D

D x V = M

Copyright ©2015 Edumedia LLC
skoool haqqında Tərəfdaşlar haqqında Toxunulmazlıq və Təhlükəsizlik
EDUMEDIA şirkəti tərəfindən adaptasiya olunub.