skoool™.az

skoool-un dərslərinə tez keçid.

Mikrodalğalar

Fotosintez prosesində yarpağın rolu

Elektromaqnit radiasiyası

« geri

Hərəkətin izahı və ölçülməsi (yuxarı)

Orta sürət | Məsafə-vaxt qrafiki | Tezlik-vaxt qrafiki | Təcil və Tormozlama

Orta sürət

İstənilən gedişdə nəqliyyat vasitəsinin sürəti dəyişkən olacaq, amma onun orta sürəti götürülmüş ümumi məsafə və vaxt bilindikdə hesablana bilər.

Orta sürət (m/san)

Gedilən məsafə (m)
Götürülmüş vaxt (san)

Beləliklə, velosipedçi dəqiqədə (60 saniyə) 600 metr hərəkət edirsə, onun orta sürəti:

	Orta sürət	=	600 60
		=	10 m/san

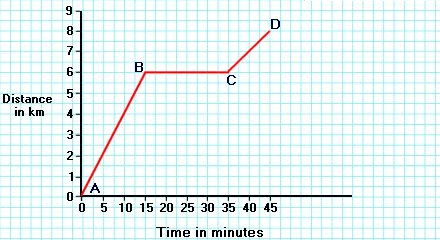
Məsafə-vaxt qrafiki

Obyekt düz xətt üzrə hərəkət edirsə, onun müəyyən nöqtədən məsafəsi məsafə-vaxt qrafiki kimi göstərilə bilər. .

A-B xətti dəyişməz sürətlə hərəkət edən maşını göstərir. O hər 5 dəqiqədə 2 km qət edir.

C-D xətti də dəyişməz sürəti göstərir, amma o daha yavaş gedir və hər 5 dəqiqədə 1 km qət edir.

Yamacın əyilmə bucağı obyektin sürətini verir.

Əyilmə bucağı	=	Qət edilmiş məsafə time taken

Gradient of line A-B	=	6 km 15 minutes

	=	0.4 km/min

Gradient of line C-D	=	2 km 10 minutes

	=	0.2 km/min

The steeper the slope of the graph, the greater the speed it represents.

The horizontal line, B-C, shows that the car has stopped.

The distance stays at 6 km from where the car set off.

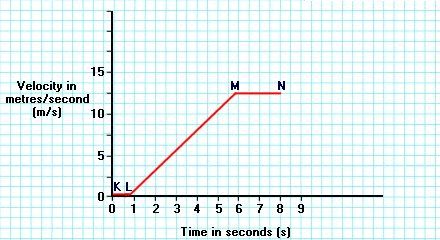
Velocity–time Graph

Velocity is speed in a given direction.

Velocity-time graphs can represent the movement of an object.

Between K and L the velocity of the car is 0 m/s. It is stopped.

Between L and M the car's velocity is increasing at a constant rate. Every second its velocity increases by 2.5 m/s.

A diagonal line shows an object is moving with constant acceleration.

The gradient of the line gives the acceleration.

Gradient of L-M	=	change in velocity time taken

	=	12.5
		5

	=	2.5 m/s²

The steeper the slope of the line, the greater the acceleration.

Between M and N the velocity stays at 12.5 m/s.

A horizontal line shows a constant velocity.

The area under a velocity-time graph represents the distance travelled.

Area under line L-M	=	½ x height of triangle x base of triangle
	=	½ x 12.5 x 5
	=	31.25

So the car covered 31.25 m whilst accelerating.

The area under line M-N	=	height of rectangle x width of rectangle
	=	12.5 x 2.2
	=	27.5

So the car travelled 27.5 m at a constant velocity.

The total distance travelled	=	31.25 + 27.5
	=	58.75 m

Acceleration and Deceleration

Acceleration is the rate at which the velocity of an object changes.

This equation is used to calculate the steady acceleration of an object, travelling in a straight line.

acceleration (m/s²)	=	change in velocity (m/s)
		time taken for change (s)

If a car accelerates from a velocity of 10 m/s to 50 m/s in 5 seconds its acceleration will be:

Acceleration	=	(50 -10)
		5

	=	40
		5

	=	8 m/s²

The rate that an object's velocity decreases is called its deceleration.

It is calculated using the same equation.

If a car is travelling at 20 m/s and it comes to a halt in 5s, its deceleration is:

Deceleration	=	(20 – 0) 5
	=	20 5
	=	4 m/s²

Copyright ©2015 Edumedia LLC
skoool haqqında Tərəfdaşlar haqqında Toxunulmazlıq və Təhlükəsizlik
EDUMEDIA şirkəti tərəfindən adaptasiya olunub.